
Las ecuaciones de primer grado, también llamadas ecuaciones lineales, son uno de los primeros artificios matemáticos que se nos atascan en el colegio. A pesar de ser de las ecuaciones más básicas, a muchos alumnos les cuesta interpretar la información abstracta que contienen. Hemos preparado esta guía para ver qué son estas ecuaciones, cómo resolverlas y algunos recursos útiles.
¿Qué es una ecuación de primer grado?
Lo primero que necesitamos saber para entender una ecuación es saber que todas tienen siempre la misma estructura: dos miembros separados por el signo “=”:
- El primer miembro, a la izquierda.
- El igual, en el centro.
- Y el segundo miembro, a la derecha.
¿Qué significa esto? Que lo que hay en el primer miembro tiene que ser igual a lo que hay en el segundo miembro. Si tenemos una ecuación que dice “x ? 1= 2 + 3”, entonces significa que la operación “x ? 1” nos va a dar “2 + 3”. El primer miembro es “x ? 1”, y el segundo miembro es “2 + 3”.
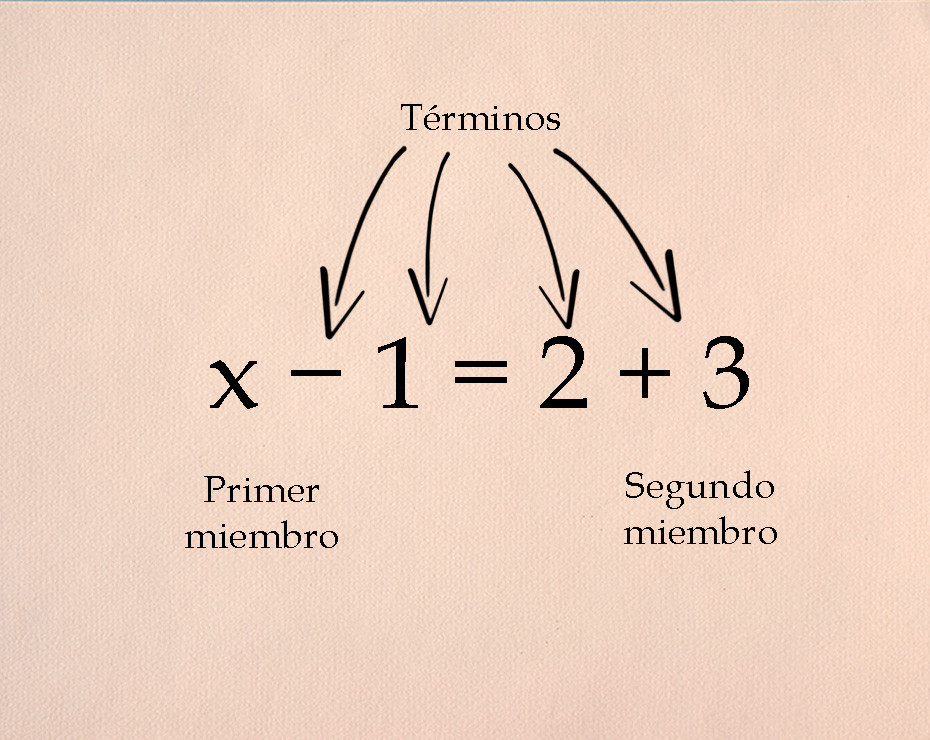
Cuando hablamos de ecuaciones de primer grado, nos referimos a aquellas en que sus variables (las incógnitas x, y, z…) cumplen varias reglas:
- Las variables no se multiplican entre sí ni se dividen. Así, la ecuación “x/y=1” no es de primer grado, pero la ecuación “x ? y = 1” sí que lo es. Las variables sí pueden estar multiplicadas por un número distinto de 1. Así, las siguientes ecuaciones son de primer grado:
-
- 2x = 3
- x + y = 2/3
- ? x ? 4y + 2z = 0
- Todas las variables están elevadas a 1 o primera potencia. Sin necesidad de entender qué significa esto, podemos comentar que la ecuación “x2 = 3” no es una ecuación lineal porque la x está elevada a “2” (segunda potencia). Estos son ejemplos de ecuaciones no lineales:
-
- x3 = 1
- x + 2y2 = 0
- x/y + z4 = 2
Una vez que tenemos claro qué es una ecuación de primer grado (y qué no), podemos aprender los mecanismos con los que se resuelven.
¿Cómo se resuelve una ecuación de primer grado?
Cuando un profesor nos pide “resolver la ecuación”, lo que pide es despejar todas las incógnitas o variables. Es decir, que descubramos cuánto vale cada variable: cuánto vale la x, cuánto vale la y, cuánto vale la z, etc. Para ello hay diferentes métodos, especialmente en el caso de ecuaciones de primer grado con más de una variable. Pero empecemos por lo fácil.
Resolver ecuaciones de primer grado de una variable
“x + 1 = 3” es una ecuación de primer grado de una variable. Además de cumplir las dos reglas que hemos visto arriba (la x está elevada a 1 y no multiplica a ninguna otra variable), la x está sola y no hay ninguna otra variable.
Este tipo de ecuaciones son muy fáciles porque su resolución solo exige pasar términos de un lado a otro, como muestran las dos reglas escritas abajo en negrita.
Cuando pasamos los términos de un lado a otro del igual, les cambiamos de signo para que la igualdad se siga cumpliendo. Por ejemplo “2 + 1 = 3”, y si queremos pasar el término “+1” al otro lado, entonces “2 = 3 ? 1”. ¿Qué pasa si no le cambiamos el signo? Que obtenemos un sinsentido: “2 ? 3 +1”.
Por tanto, para resolver la ecuación de arriba, seguimos estos pasos:
x + 1 = 3
x = 3 ? 1
x = 2
Cuando pasamos lo que multiplica a la variable al otro lado, pasa dividiendo, y viceversa. Veamos otros dos ejemplos.
| Ejemplo 1
2x + 3 = 0 2x = ?3 x = ?3/2
|
Ejemplo 2
x/2 ? 1 = 1 x/2 = 1 + 1 x/2 = 2 x = 2·2 x = 4 |
¿Por qué no hemos pasado el 2 de la ecuación de la izquierda al otro lado antes que el 3? Porque primero tenemos que tener aislada la variable.
Resolver ecuaciones de primer grado de dos variables
Para resolver una ecuación de primer grado de dos variables hacen falta dos ecuaciones. Como estas de abajo:
2x + 3y = 0
x ? y = 4
¿Cómo se resuelven estas ecuaciones? Hay tres formas diferentes: el método de sustitución, el método de reducción y el método de igualación. Sin embargo, vamos a ver solo el primer método por dos motivos: es el más sencillo de aprender, es el más sencillo de explicar y resuelve todos los casos.
El método de sustitución consiste en elegir una de las dos ecuaciones y aislar una de las variables. Por ejemplo, hemos aislado la x en la segunda ecuación, dejando la primera como estaba:
2x + 3y = 0
x = 4 + y
Ahora que sabemos que la x vale “4 + y”, vamos a sustituir ese valor en la primera ecuación, y a operar hasta despejar la y. Operamos sumando las y con las y, las x con las x, y los términos independientes con los términos independientes:
2·(4 + y) + 3y = 0
8 + 2y +3y = 0
8 + 5y = 0
5y = ? 8
y = ? 8/5
Bien, ya sabemos lo que vale la y. Ahora podemos ir a la ecuación en la que despejamos la x, sustituir el valor de y y operar:
x = 4 + (? 8/5)
x = 4 ? 8/5
x = 5·4/5 ? 8/5
x = (20 ? 8)/5
x = 12/5
Hemos elegido ecuaciones con resultados “raros” para que tengáis un ejemplo de cómo se opera hasta resolver todas las incógnitas.
Resolver ecuaciones de primer grado de tres variables
Como en el caso anterior, si queremos resolver tres incógnitas necesitamos tres ecuaciones. Por ejemplo, estas:
3x + 2y + z = 1
5x + 3y + 4z = 2
x + y ? z = 1
¿Podemos aplicar el método de sustitución? Lo cierto es que sí. De la última ecuación, “x = 1 ? y + z”. Sustituimos en la primera y segunda ecuación esta x y nos queda:
3·(1 ? y + z) + 2y + z = 1
5·(1 ? y + z) + 3y + 4z = 2
Aunque parezca algo muy enrevesado, si nos ponemos a operar llegamos a algo que ya conocemos de antes: un sistema de dos ecuaciones con dos incógnitas:
3 ? 3y +3z + 2y + z = 1
5 ? 5y + 5z + 3y + 4z = 2
———————————-
3 ?y + 4z = 1
5 ?2y + 9z = 2
———————————-
?y + 4z = ? 2
?2y + 9z = ?3
Ahora, basta con volver a aplicar el método de sustitución, por ejemplo separando la y de la primera ecuación (“y = 4z +2”) y sustituyendo en la segunda:
?2·(4z + 2) + 9z = ?3
?8z ? 4 + 9z = ?3
z ? 4= ? 3
z = ? 3 + 4
z = 1
Ya tenemos el valor de z. Ahora retrocedemos un paso y sustituimos este valor en la ecuación con la y despejada:
y = 4·1 +2
y = 6
Con dos incógnitas despejadas, podemos seguir retrocediendo y usar ahora la ecuación en la que teníamos la x despejada:
x = 1 ? 6 + 1
x = ? 4
Una calculadora online para salir de dudas
Si estamos estudiando las ecuaciones de primer grado, nos vendrá muy bien practicar. Para ello, tener ejercicios resueltos resulta indispensable. La Calculadora de ecuaciones de Symbolab puede echarnos una mano con esto, sin importar la complejidad.
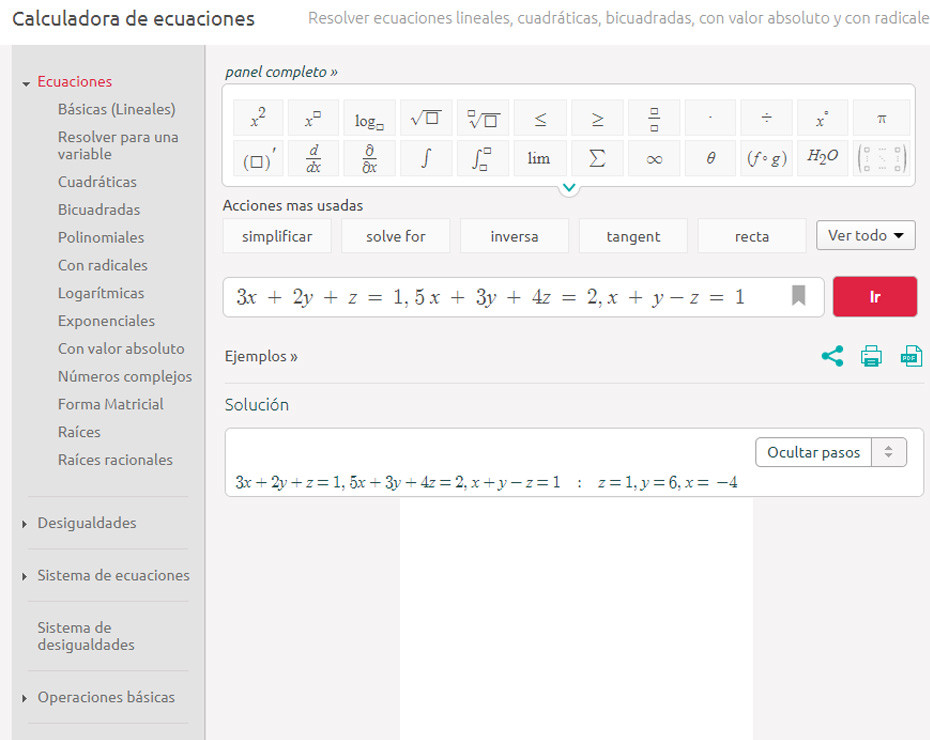
Bastará con rellenar la celda delante de “Ir” con nuestra ecuación o sistemas de ecuaciones. Si son varias ecuaciones, las separamos con comas. La ventaja de esta página web es que, además de la solución, le podemos pedir los pasos, por lo que podremos aplicar razonamiento inverso para descubrir otras formas de resolver las ecuaciones.
La misma web, en la parte inferior, incorpora para ecuaciones de una o dos variables una gráfica que muestra las ecuaciones en el plano.
En Nobbot | ¿Arte o matemáticas? Las simetrías ocultas de la tabla de multiplicar
Imágenes | Propias


Excelente
Interesante el tema, y que sugiere su esfuerzo. Gracias
Esta información está bien echa y me ayudó a comprender más del tema