 Si ahora te pusieran una raíz cuadrada, ¿serías capaz de resolverla? Si recuerdas el proceso, enhorabuena; si no, nunca es tarde para refrescar las operaciones matemáticas que aprendiste en el colegio.
Si ahora te pusieran una raíz cuadrada, ¿serías capaz de resolverla? Si recuerdas el proceso, enhorabuena; si no, nunca es tarde para refrescar las operaciones matemáticas que aprendiste en el colegio.
Índice
- Raíz cuadrada: definición, elementos y cómo hacer una raíz cuadrada
- ¿Cuál es la diferencia entre una raíz cuadrada exacta y otra entera?
- Historia y origen del símbolo de la raíz cuadrada
- Raíces cuadradas útiles: la del dos, tres y cinco
Raíz cuadrada: definición, elementos y cómo hacer una raíz cuadrada
La raíz cuadrada de un número es la operación matemática a partir de la cual el número resultante multiplicado por sí mismo permite obtener el número inicial. Es importante distinguir los elementos que la forman:
- Índice: este número es el que índica a qué está elevada la raíz cuadrada. En nuestro caso, este índice es dos pero si, por ejemplo, hablamos de una raíz cúbica, sería el tres.
- Radical: se corresponde con el símbolo a través del cual se identifica la operación, ?.
- Radicando: se coloca debajo del radical y es el número sobre el que se calcula la raíz cuadrada.
- Renglones auxiliares: en esta zona, a la derecha, se van colocando todos los números que ayudan a hacer la raíz cuadrada.
- Raíz: es el número que resulta de calcular la raíz cuadrada del radicando.
- Resto: puede ser cero o cualquier otro número. El resto ‘cierra’ la raíz cuadrada.
Tras haber definido qué es una raíz cuadrada y sus elementos, explicamos los pasos que hay que seguir para calcularla con el siguiente ejemplo: ?28764
- Primero, dividimos en grupos de dos en dos cifras el número con el que vamos a trabajar. Esta división se hace de derecha a izquierda. En nuestro ejemplo, contamos con tres grupos resultantes: 2, 87 y 64.
- A continuación, hay que centrarse en el dígito que está más a la izquierda (2) y pensar qué número multiplicado por sí mismo es 2 o se aproxima lo máximo posible. En este caso, la solución es 1. Una vez averiguada la solución, se resta su cuadrado (1) a 2. El resultado de esta operación como veis en la imagen es 1.

- Después, cogemos el segundo grupo de cifras (87) y lo colocamos al lado del resultado de la resta antes realizada (1). Trabajaremos con la cifra 187 y, para ello, en la zona de los renglones auxiliares indicamos el doble del número puesto en la raíz (1): 2.

- Llegados a este punto, toca pensar en un dígito que acompañe al número 2 de modo que ese mismo dígito lo usaremos en la operación que veis en la imagen en color verde. El concepto con el que hay que quedarse es que el resultado de esa multiplicación debe aproximarse (puede darse el caso de que se trate de un número exacto) al número que hay en la parte izquierda de la pantalla en color negro (en nuestro ejemplo el 187). El dígito que necesitamos es el 6 para luego restar el resultado de esa operación a 187. La diferencia de esta resta es 31.
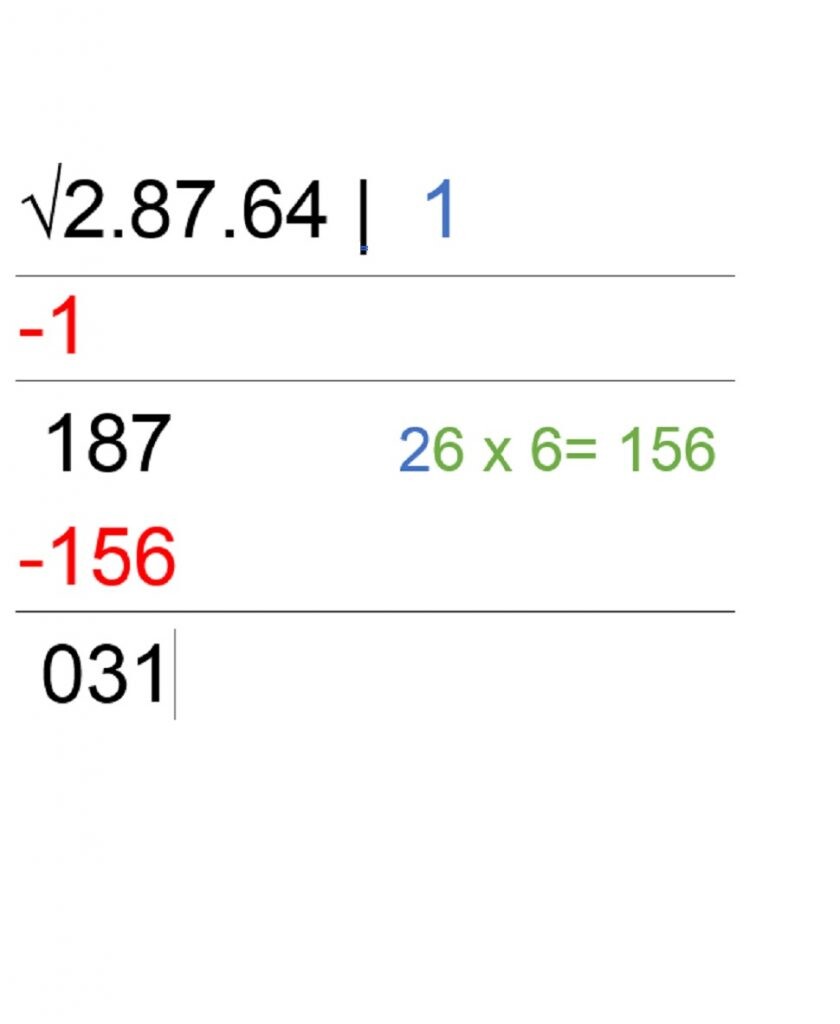
- Subimos el 6 a la zona de la raíz junto al 1 que ya tenemos. Luego, bajamos el último grupo de números (64) para colocarlos junto a la solución (31) de la operación del paso anterior. Cuando hayamos completado esta parte, calculamos el doble del número que tenemos en la raíz. Como el doble de 16 es 32, lo apuntamos como aparece en los renglones auxiliares de la siguiente captura.

- Repetimos todo el proceso que explicamos en el punto número cuatro. En esta ocasión, el número que necesitamos es el 9. Así, a 3164 le restamos la cantidad obtenida de multiplicar 329 x 9. El resultado es 203.
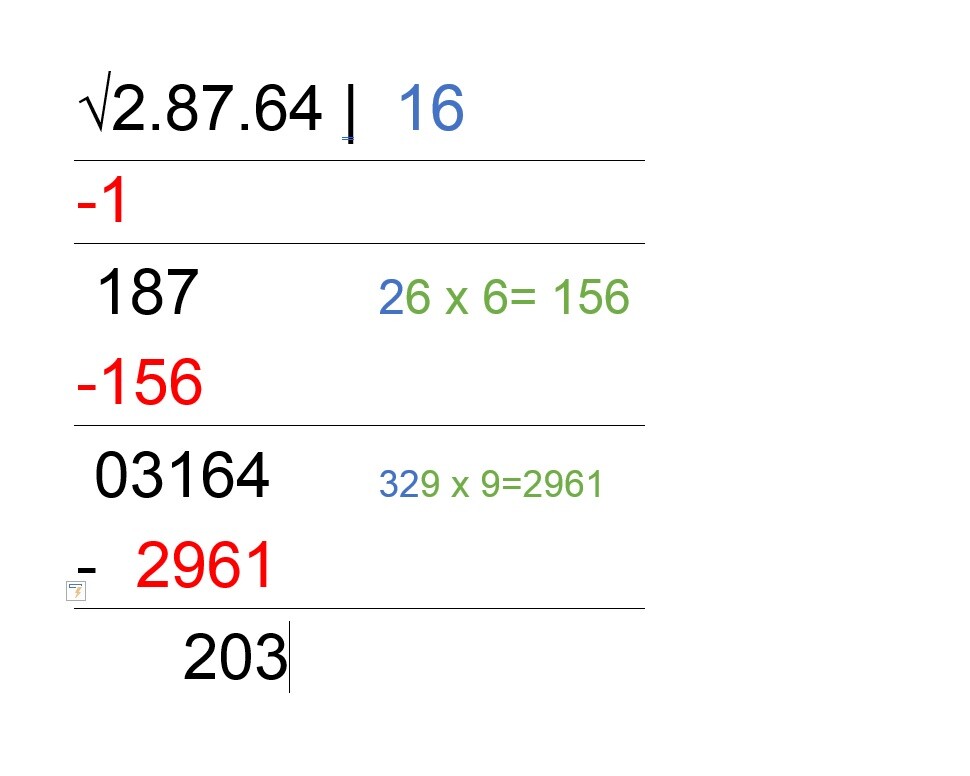
- Finalmente, sólo nos queda subir el número 9 junto al resto de dígitos que tenemos en nuestra raíz: 16. La raíz cuadrada de 28 764 es 169. Para comprobar que hemos resuelto bien el ejercicio, hay que multiplicar 169 por sí mismo y luego sumarle el resto, 203.

¿Cuál es la diferencia entre una raíz cuadrada exacta y otra entera?
El ejemplo que hemos desarrollado para explicar cómo hacer una raíz cuadrada ilustra qué es una raíz cuadrada entera. Es aquella que no tiene una raíz cuadrada perfecta: es decir, hay que multiplicar el número obtenido por sí mismo y, a continuación, sumarle el resto de la operación. Por su parte, en una raíz cuadrada exacta no es necesario sumar este resto, porque cuando multiplicamos la raíz cuadrada que hemos calculado por sí misma el resultado equivale al radicando. Estos son algunos ejemplos de raíces cuadradas exactas: ?25 igual a 5, ?36 igual a 6, ?144 igual a 12, ?400 igual a 20…
Historia y símbolo de la raíz cuadrada
Esta operación matemática tiene muchos años de historia. De hecho, existen referencias a ella en el Antiguo Egipto, la Antigua India y Babilonia. Incluso en el periodo pitagórico (desde el 600 a.C hasta el 300 d.C) ya las usaban. Si al principio sobre todo se empleaba para resolver problemas geométricos y trigonométricos, con el paso del tiempo su uso se extendió a otras áreas como los polinomios y las ecuaciones.
Por otra parte, el símbolo matemático que representa esta operación resulta cuando menos particular. El que todos conocemos se remonta al año 1525. Se encargó de introducirlo el matemático polaco Christoph Rudolff por primera vez en su libro ‘Coss’ dedicado al álgebra: es una representación estilizada de la letra r en referencia al término latino radix. que significa raíz.
Raíces cuadradas útiles: la del dos, tres y cinco
Cuando se estudian las raíces cuadradas, una de las preguntas que suelen plantearse es: ¿pero esto para qué me puede servir? Algunas como las del dos, tres y cinco son útiles en geometría. Por ejemplo, la ?2, considerada el primer número irracional (1,4142135623) descubierto, equivale a la longitud de la diagonal de un cuadrado cuyo lado es igual a la unidad. Se comprueba a través del teorema de Pitágoras.
La ?3 o constante de Teodoro, en reconocimiento a la labor del filósofo y matemático griego Teodoro de Cirene que desarrolló la teoría de los números irracionales, da como resultado 1,7320508075; en geometría, la diagonal de un cubo cuyos lados miden 1 equivale a la raíz cuadrada de 3. Mientras, la ?5 se corresponde con la hipotenusa de un triángulo cuyos catetos miden 1 y 2 respectivamente. Esta raíz cuadrada aparece en la fórmula del número áureo, un número irracional que se representa a través de la letra griega ? (phi) (si es minúscula) o ? (Phi) (si es mayúscula) en homenaje al escultor griego Fidias. La ?5 es 2,2360679774.
En Nobbot | Carmen Izquierdo (Kotokan): «Las matemáticas son la asignatura que enseña a razonar de forma lógica»
Imágenes | Gerald/Pixabay (apertura), Clker-Free-Vector-Images/Pixabay, propias


Excelente artículo, ya estoy en universidad y ahora que le estoy ayudando a una primita a estudiar, necesitaba recordar esto. Muy interesante y bonito que agregue la historia de porqué se le dice «raiz».