¿Cuándo vamos a resolver “los grandes problemas matemáticos” del milenio?

Cada pocos años un matemático aparece plantando una solución a una gran incógnita y el mundo se pone patas arriba. No debería sorprender a nadie: el trabajo del matemático es esencialmente ese.

Por desgracia, no todas las soluciones están premiadas con el mismo ímpetu: un millón de dólares para cada uno de los grandes problemas del milenio. ¿Y de qué tratan esos grandes e irresolubles problemas?

EL DINERO ES SÓLO UN PRETEXTO

Relacionado

• 
  Algoritmo, la nueva palabra mágica: ¿qué son y hasta qué punto van a condicionar nuestras vidas?

Antes de nada, un poco de contexto: en la conferencia de París del Congreso Internacional de Matemáticos de agosto de 1900, el matemático alemán David Hilbert presentó una lista con 23 problemas que consideró entonces los más importantes para las matemáticas. Cien años después, con algunos resueltos, otros desestimados y algunos más convertidos en problemas más grandes, esos 23 se convirtieron en 7.

El consenso generalizado los transformó en pequeños anatemas, en ballenas blancas a cazar. Y el Clay Mathematics Institute, institución sin ánimo de lucro creada por el millonario bostoniano Landon T. Clay, empujó el ímpetu con una golosina adicional: el citado millón de dólares por cada solución.

Los Millennium Prize Problems habían tomado forma a través de un oneroso galardón —gala incluida, claro— que ni el Nobel alcanza. Pero el dinero es un simple pretexto. La necesidad de resolución, el deseo profesional, el mérito laboral y otros logros intangibles convierten estas metas en coronas sin dueño.

LA CONJETURA DE POINCARÉ

Empecemos por la buena noticia. Tan sólo seis años después de poner sobre la mesa esos millones de dólares para cada incógnita sin resolver, el ruso Grigori Perelman dio con la clave de la conjetura de Poincaré. Más de un siglo de incertidumbre y este héroe no quiso ni recoger su cheque, ni su medalla Fields, ni aparecer por las esferas académicas.

Porque para explicar esta conjetura hemos de pensar en una esfera —una hueca, un cascarón vacío—. La superficie es conexa. Según la conjetura de Poincaré, esta afirmación valdría también para esferas tridimensionales. ¿Para todos los valores? ¿Todas son esferas cuatridimensional? ¿Todas se pueden reducir a un simple punto?

Encontrar la solución ha servido para estudiar y simular, de forma más exacta, el comportamiento replicante de tumores: dentro de las matemáticas geométricas, esta conjetura ha dado pie a nuevas investigaciones sobre los agregados multicelulares esféricos.

P CONTRA NP

¿Y si los problemas más complicados son en realidad problemas simples disfrazados? Pensemos en la sintaxis de la lengua: una oración puede contener 50.000 caracteres, estar copada de subordinadas y núcleos satelitales, como muchos planetas orbitando en torno a una única gran estrella. ¿Podría darse este caso a la hora de analizar las clases de complejidad entre problemas de tipo P y de tipo NP?

No, según su definición formal de 1971. Estaríamos hablando de una fórmula distinta. De hecho, Norbert Blum lanzó desde la Universidad de Bonn una certeza: P no es igual a NP. Aunque todas las respuestas han sido perecederas, poco conclusivas. Y la de Blum parece contener una serie de errores sutiles que la desbaratan.

Por su carácter exponencial, este problema aritmético aún no ha encontrado solución. Y es que si se resolviera de forma afirmativa significaría que la encriptación y ciberseguridad en Internet no es lo que asegura ser. El esquema actual se desmoronaría. El de P versus NP parece ser más un problema de falta de herramientas que de capacidades de síntesis analítica. ¿Cuál es el límite de la computación?

LA CONJETURA DE HODGE

La conjetura de Hodge dice que,«para variedades algebraicas proyectivas, los ciclos de Hodge son una combinación lineal racional de ciclos algebraicos». Te has quedado igual, ¿verdad? Al tratarse matemáticas complejas, es imposible descifrarlo sin un conocimiento previo. Aquí puedes encontrar un fenomenal resumen. Y ya existen un puñado de intentonas intentando darle sentido. Cuanto ni menos darle solución.

El matemático belga Pierre Deligne, padre también de la teoría K, fue quien formuló este problema de geometría algebraica donde, si todo ciclo es una combinación racional de ciclos algebraicos —asociados a subvariedades analíticas cerradas, fuente de una lógica intrínseca—.

Es común leer que esta conjetura enhebra otras tantas y su solución sería un «tirar de la manta» en varios postulados de matemáticas abstractas que encuentran enemigos comunes en Hodge. Sobre la practicidad de la misma, el maestro alemán Karl Weierstrass lo explica bastante bien:

«A la pregunta de si es realmente posible sacar provecho alguno de las teorías abstractas que la matemática moderna parece apoyar, uno debería contestar que fue basándose únicamente en la especulación pura cómo los matemáticos griegos dedujeron las propiedades de las cónicas, mucho antes de que nadie pudiera imaginarse que representan las órbitas de los planetas». Bueno, en realidad se trata de curvas geodésicas, pero nos entendemos.

LA HIPÓTESIS DE RIEMANN

«La hipótesis de Riemann dice que todos los ceros no triviales de la función zeta de Riemann tienen una parte real de 1/2». No, a ver, empecemos desde el principio. Pensemos en el teorema fundamental de la aritmética, esa que dice que cualquier número se puede expresar de forma única como producto de potencias de números primos.

Esto nos recuerda una máxima: los números primos son infinitos. ¿No tenemos una regla de divisibilidad básica? Bueno, tenemos la criba de Eratóstenes. Pero, entre nosotros, es un mero juguete y no sirve para encontrar números primos gigantescos.

Algunos números tienen la propiedad especial de no poder expresarse como producto de dos números más pequeños. Son llamados números primos. Los números naturales no siguen un patrón. Sin embargo, el matemático Bernhard Riemann observó grupos, un comportamiento a través de una función, la denominada función zeta de Riemann ?(s), donde conjeturó la distribución de los ceros.

Pese a unos pocos escépticos, la comunidad está de acuerdo en esta conjetura, pero aún no ha podido demostrarla. De hecho esta hipótesis habla de una distribución factorial, de una regla interna que nos diga qué valores complejos de s hacen de ?(s)=0. Este problemas ya formó parte de los 23 planteados por Hilbert en el Congreso Internacional de matemáticos de 1900 y darle solución, prometen algunos, podría ayudarnos a comprender tanto el universo de las matemáticas como de todo cuanto nos rodea.

EXISTENCIA DE YANG-MILLS Y DEL SALTO DE MASA

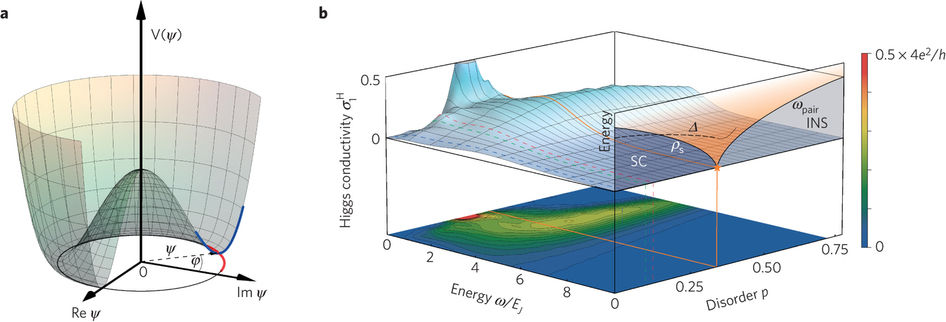
Si la teoría de la relatividad ha servido para que un GPS pueda posicionar correctamente la dirección a la que nos dirigimos (3D), esta teoría podría dar respuesta a cuestiones espaciales en cuatro dimensiones. Pero el problema se encuentra en punto muerto. Ni siquiera se ha podido demostrar que existe, aunque se deduce.

Los físicos más conservadores se han posicionado hacia otro tipo de escenarios —donde el bosón de Higgs responde a muchas preguntas—. En física es común escuchar que uno encuentra, gran parte de las veces, lo que busca. Es decir, a veces nuestra propia mirada distorsiona lo que vemos. Y viceversa.

La formulación oficial, cortesía de Arthur Jaffe y Edward Witten, dice que el salto de masa (mass bandgap) trata de explicar por qué la interacción fuerte es una interacción de corto alcance. Los físicos Chen Ning Yang y Robert Mills son los responsables de esta singularidad. Ellos sugirieron que la no-variación de gauge local no es compatible con una teoría de campos local: debe existir una simetría, una correlación lógica. Otro millón de dólares le espera a quien resuelva la contradicción.

¿Y qué hay que explicar? Cómo un estado ha adquirido masa y, de paso, explicar por qué los bosones vectoriales débiles tienen una gran masa en reposo. Ah, y que esta respuesta concuerde tanto en interacciones fuertes como débiles. No, no parece que vayamos a dar con la solución mañana mismo.

LAS ECUACIONES DE NAVIER-STOKES

Algunos problemas sólo crecen cuando se intenta desenterrar la raíz de los mismos. Las ecuaciones de Navier-Stokes cuentan con más de un siglo de solera y describen el movimiento de líquidos y gases sobre espacios definidos (como tuberías). El enunciado del problema afirma que debe existir una respuesta sencilla a partir de la cual podríamos encontrar solución a cada estado en el tiempo en el que esa materia está fluyendo.

Una vez más se trata de dar forma a las derivas parciales. Y, una vez más, contamos con una solución parcial. El profesor Kazaja Mujtarbay Otelbáyev explicó su hallazgo en La existencia de una buena solución de la ecuación Navier-Stokes. Los medios rusos se congratularon con la propuesta, pero ésta no ha sido considerada como definitiva. Y es que no parece tan sencillo: hay que tener en cuenta una gran cantidad de variables físicas (supercriticidad), entre las que se incluye la resistividad del elemento conductor. No hay atajos posibles.

La pregunta pertinente, una vez más es, ¿para qué serviría dar solución a estas ecuaciones? Para un montón de cosas. La simulación de fluidos ahorra enormes costes de producción en películas o videojuegos (*computational fluid dynamics*). A través de estas fórmulas también conoceríamos con mayor exactitud cómo se comportan ciertas fluidos ante ciertos situaciones anómalas. Sí, estamos pensando en situaciones fuera del planeta, en plena conquista espacial.

CONJETURA DE BIRCH Y SWINNERTON-DYER

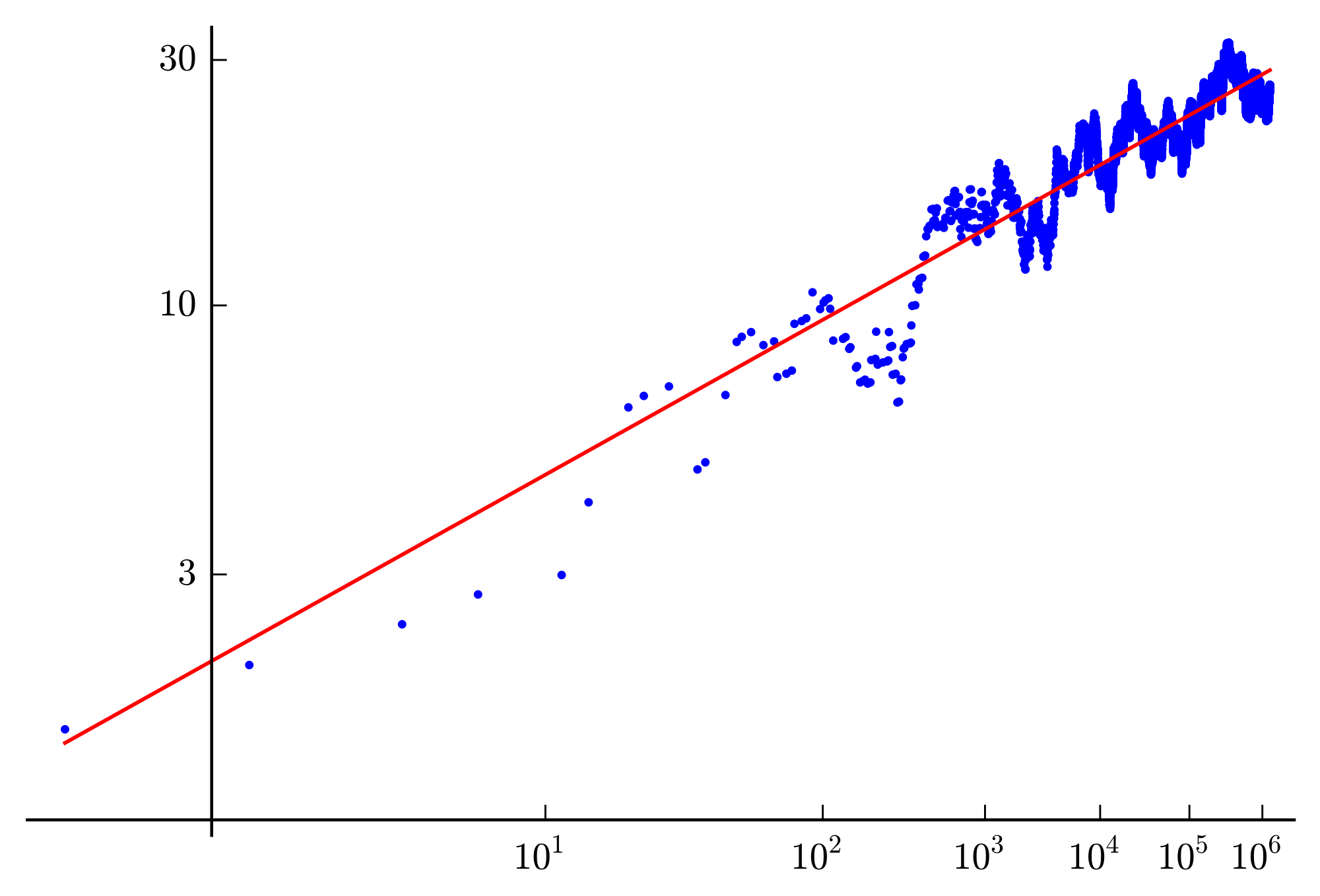
Abreviado dentro del círculo académico como BSD, este es quizá el problema más próximo a su resolución. De hecho, ya cuenta con dos respuestas, sobre dos elipses concretas. Sí, volvemos a las elipses. Pero es que la conjetura planteada asegura que existe una forma sencilla de averiguar si el tipo de ecuaciones que definen las curvas elípticas tienen un número finito o infinito de soluciones.

Enunciada en 1965 por los matemáticos ingleses Bryan Birch y Peter Swinnerton-Dyer, las principales aproximaciones han llegado por diversas manos y tintas, aunque una destaca sobre el resto: Andrew J. Wiles (Cambridge, 1953). Este matemático británico saltó a la palestra cuando expuso la demostración del último teorema de Fermat —en primera instancia resultó fallida pero él mismo lo corrigió durante el verano de 1995—.

El investigador de Princeton Francesc Castellà es otra de las mentes preclaras que bucean en la resolución de la conjetura. ¿Y para qué nos serviría darle respuesta? Las posibilidades son ambiguas. Si la resolución de ‘P contra NP’ podría desencadenar una brecha en la criptografía, la resolución de esta otra conjetura podría servir para plantear nuevos modelos de seguridad.

En cualquier caso, hoy gozamos de un mayor conocimiento en fragmentación y compresión digital de archivos gracias al desarrollo de ondículas. En las matemáticas, no es necesaria una relación directa entre la solución del problema y su implantación en la sociedad mediante un modelo práctico. Las matemáticas son, en sí mismas, la solución.

En Nobbot | Borja Sorazu, físico: “Con la detección de ondas gravitacionales abrimos una puerta a lo desconocido”

Imágenes | Pexels, Wikipedia, (cabecera de ‘Good Will Hunting‘, Miramax Films)