
Los problemas de máximo común divisor y mínimo común múltiplo están por todas partes en nuestro día a día. Por ejemplo, en el problema de las salchichas y los panes a la hora de hacer perritos calientes. Para resolverlos solo hace falta un lápiz y un papel. Y, sin embargo, es de ese tipo de operaciones que parecen muy complicadas por su procedimiento.
La realidad es que apenas lleva unos minutos resolver uno de estos problemas. En este artículo se verá qué es el máximo común divisor y mínimo común múltiplo, sus diferencias y en qué consiste su descomposición o factorización de números. Y, lo más importante, se verán problemas de máximo común divisor y mínimo común múltiplo resueltos.
Índice
- ¿Qué es el máximo común divisor?
- ¿Qué es el mínimo común múltiplo?
- Cómo factorizar números
- ¿Cómo calcular el máximo común divisor?
- ¿Cómo calcular el mínimo común múltiplo?
- Problemas de máximo común divisor y mínimo común múltiplo
¿Qué es el máximo común divisor?
El máximo común divisor (M.C.D.) es el máximo número entero que divide a dos o más números sin dejar resto en la operación de división. Como ejemplo, el máximo común divisor de los números 20 y 30 es 10. Este es el mayor entero posible que divide a ambos (20 y 30) devolviendo a su vez números enteros:
20/10 = 2
30/10 = 3
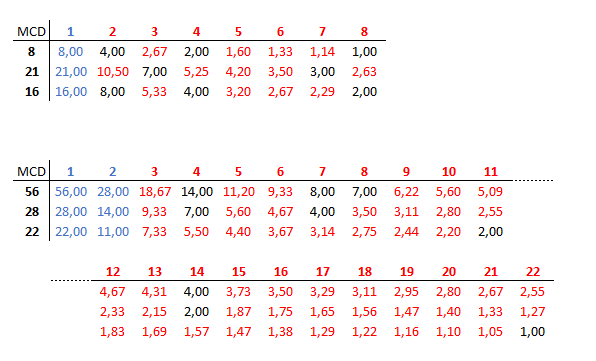
¿Qué pasa con los enteros intermedios como 1, 2, 3… 20 que no cumplen alguna de las condiciones del M.C.D.? En la siguiente tabla se muestran todas las divisiones posibles para estos números: (20/1 = 20), (20/2 = 10); (20/3 = 6,67), etc. y sus respectivos resultados.

En rojo se muestran aquellos números enteros que no dan un resultado entero al dividir a 20 o 30 y, por tanto, están descartados como válidos para el M.C.D. En azul se marcan aquellos números que sí que cumplen que la división sea entera, pero solo cuando lo cumplen para ambas cifras (en este caso, 20 y 30).
Así, se puede ver que tanto 20 como 30 son divisibles entre 1, 2, 5 y 10 dando como resultado números enteros. Pero el M.C.D. es solo un número, no varios. ¿Cuál es la mayor de estas cifras? 10. De modo que 10 es el máximo común divisor de 20 y 30.
El máximo común divisor se puede calcular también para más de dos cifras. En los ejemplos de abajo se muestra el MCD de 8, 16 y 21 (1), y de 56, 28 y 28 (2). Por descontado, existe una forma mucho más sencilla de calcular el máximo común divisor, que se verá más adelante.
¿Qué es el mínimo común múltiplo?
El mínimo común múltiplo (m.c.m.) de dos o más números es el número entero más pequeño múltiplo de todos ellos. Por ejemplo, el mínimo común múltiplo de 3 y 5 es 15, porque no existe ningún número entero menor de 15 que pueda dividirse entre 3 y entre 5 dando como resultado un número entero.

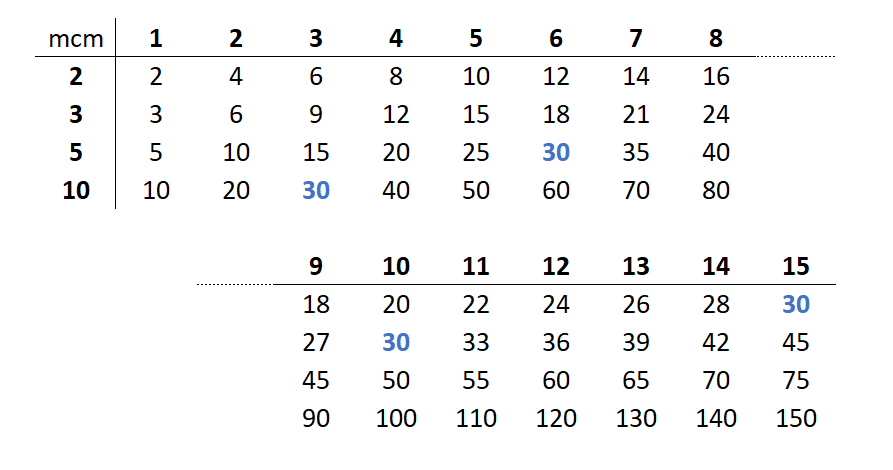
En este caso la tabla de arriba muestra las tablas de multiplicar del 3 y del 5 puestas en línea: (1·3 = 3); (2·3 = 6); (3·3 = 9), etc. La primera fila muestra todos los múltiplos de 3, y la segunda todos los múltiplos de 5. En azul, los múltiplos que están en ambas tablas de multiplicar. Entonces, ¿cuál es el múltiplo común más pequeño? El 15. Luego el 15 es el mínimo común múltiplo entre 3 y 5.
De nuevo, este procedimiento puede usarse con más de dos números. Abajo se puede observar cómo el mínimo común múltiplo de 2, 3, 5 y 10 es 30, porque es el primer número que aparece compartido en todas las tablas. Por supuesto, hay formas más fáciles de calcularlo, y todas pasan por la descomposición o factorización de números.
¿En qué se diferencian los problemas de máximo común divisor y mínimo común múltiplo?
Se trata de dos procedimientos diferentes con objetivos distintos. El máximo común divisor se aplica a problemas en los que aparecen cocientes, divisiones, repartos o porcentajes; mientras que el mínimo común múltiplo se usa en problemas en los que hace falta buscar un mínimo común a varios números y por tanto multiplicaciones y números grandes.
Cómo calcular los factores de cada número (descomponer números)
En un problema se pide calcular tanto el máximo común divisor como el mínimo común múltiplo de 10 y 15. Lo interesante es que ambos cálculos pasan por la factorización de estos dos números. En otras palabras, calcular los números primos que, multiplicados, dan lugar a numerador y denominador.
Para ello, la forma más sencilla es escribir el número en cuestión en una hoja y luego trazar una línea vertical a su derecha, tal y como se muestra en la imagen (a). A continuación se empezará a dividir por el primer número primo (2) a ver si el resultado da un número entero.
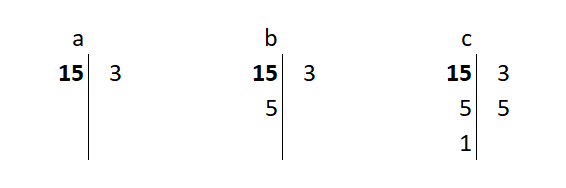
Como 10/2 = 5, y 5 es un número entero, entonces se escribe el 2 a la derecha y el 5 bajo el 10 (b). Y se repite el procedimiento. ¿Es 5 divisible entre 2? No, porque no da un número entero. ¿Es 5 divisible entre 3 (siguiente número primo)? No, porque no da un número entero. ¿Es 5 divisible entre 5 (siguiente número primo)? Sí, porque da 1, que es un número entero (c). Los factores de 10 son 5·2.
Del mismo modo, se calculan los factores de 15, que son 5·3, como se muestra en la imagen de abajo:
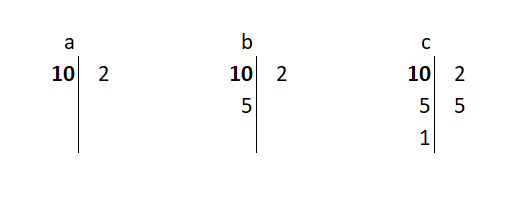
Los factores de los números se suelen ordenar de mayor a menor, y a agrupar cuando hay varios que coinciden. Por ejemplo, los factores de 1260, que son 2·2·3·3·5·7 se escriben como 22·32·5·7; y los factores de 276, que son 2·2·3·23 se escriben como 22·3·23. Es decir, se escriben en forma de potencia. Esto facilita mucho ver cuántos hay de cada uno.

¿Cómo se calcula el máximo común divisor?
Una vez factorizados dos o más números, para calcular su máximo común divisor tan solo hay que tomar los factores comunes elevados a la mínima potencia o exponente. Como ejemplo, para calcular el máximo común divisor de 1260 y 276, cuyos factores se han calculado arriba, primero habría que escoger los factores comunes. Pero, ¿cuáles son?
1260 = 22·32·5·7
276 = 22·3·23
En este caso, el 2 y el 3 aparecen en ambas factorizaciones. Por lo tanto, 2 y 3 son los factores comunes de 1260 y 276. Una vez identificados, hay que tomar solo el menor exponente de cada uno:
En el caso del 2, se observa cómo está elevado a 2 en ambas factorizaciones, así que este es fácil: se elegirá 22. Con el 3 el procedimiento es similar, pero hay que fijarse que una de las factorizaciones solo tiene un 3 (31) y la otra un 32. ¿Cuál habrá que tomar? Según la regla del máximo común divisor, el que tenga la mínima potencia: 31 o, lo que es lo mismo, 3.
Recopilando, dado que los factores comunes elevado a la mínima potencia o exponente son 22 y 31, entonces se puede concluir que el máximo común divisor de 1260 y 276 es 12, porque 12 es 22·3.
Calculadora online de máximo común divisor
En la página web de Symbolab hay una calculadora de máximo común divisor con la que se pueden realizar pruebas.
¿Cómo se calcula el mínimo común múltiplo?
Una vez factorizados dos o más números, para calcular su mínimo común múltiplo solo hay que tomar los factores comunes y los no comunes elevados a la máxima potencia o exponente. Como ejemplo, para calcular el mínimo común múltiplo de 35 y 75, primero habrá que calcular sus factores:
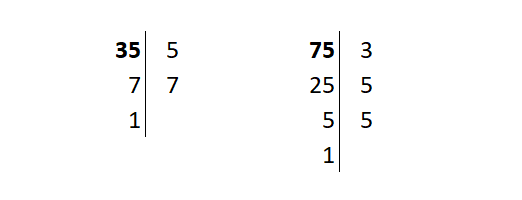
35 = 5 · 7
75 = 3 · 52
Hay que tomar tanto factores comunes como no comunes (en este caso 3, 5 y 7) y hacerlo al máximo exponente en el que aparezcan en la factorización. Es decir, 31, 52 y 71. El mínimo común múltiplo de 35 y 75 será 525 = 31·52·71.
Calculadora online de mínimo común múltiplo
En la página web de Symbolab hay una calculadora de mínimo común múltiplo con la que se pueden realizar pruebas.
problemas de máximo común divisor y mínimo común múltiplo
Problema 1. Alba acude a la compra cada cinco días, mientras que José lo hace cada ocho días. Si hoy han coincidido, ¿cuándo volverán a hacerlo?

Antes de aplicar fórmulas, hay que determinar si estos problemas son de máximo común divisor o de mínimo común múltiplo. De modo que se plantea el problema usando algo de lógica.
Alba ha acudido hoy a comprar y, como va cada cinco días, también irá el día 5, el 10, el 15, etc. José acudirá el 8, el 16, el 24, etc. Se trata de un problema de mínimo común múltiplo porque hay que buscar el primer día que volverán a coincidir (el día ‘mínimo’):
Ahora, ¿cómo se resuelve usando la fórmula del m.c.m.? Primero habrá que factorizar y, luego, tomar factores comunes y no comunes al mayor exponente.
5 = 51
8 = 23
En este caso es muy fácil. Los factores son 5 y 2, y elevados a los exponentes máximos son 51 y 23. Alba y José coincidirán el día 40 porque 40 = 51 · 23.
Problema 2. Los paquetes de salchichas tienen cinco unidades cada uno, pero los de pan tienen seis. ¿Cuántos paquetes hay que comprar para gastar lo mínimo posible pero que no sobre ni una salchicha ni un pan?
De nuevo se está ante un problema de mínimo común múltiplo. ¿Por qué se sabe? Porque se busca un mínimo de compras. Al factorizar queda:
5 = 51
6 = 3 · 2
Aplicando la fórmula del m.c.m., se observa que el resultado es: 5 · 3 · 2 = 30. Pero 30 no es la solución. 30 es el número mínimo de salchichas y panes. Habrá que comprar seis paquetes de salchichas (30 en total) y cinco paquetes de panes (30 en total). Así no sobrará ninguno.
Problema 3. Se dispone de tres cuerdas de 50, 75 y 125 metros de largo, respectivamente, y se desea cortarlas de forma que sus trozos sean lo más largos posibles pero que a su vez sean iguales. ¿Cuánto medirá cada trozo?

En este caso es fácil entender que se busca una división porque la cantidad buscada es inferior a 50, 75 y 125 (no se puede cortar una cuerda en una longitud más grande que esta). De modo que primero toca factorizar:
50 = 2 · 52
75 = 3 · 52
125 = 53
Ahora, aplicando la fórmula, hay que tomar los elementos comunes elevados al menor exponente. Dado que el único número que coincide es el 5, y el exponente mínimo es el 52, entonces cada cuerda medirá 52 = 25 metros. Era algo que, para este caso concreto, se podría haber calculado de cabeza.
Problema 4. En un evento se reparten 40 bolígrafos y 16 pines. El objetivo es hacer el mayor número de packs posible de forma que todos contengan el mismo número de elementos. ¿Cuántos packs habrá?
Se trata de un problema de máximo común divisor porque se busca maximizar el contenido de cada pack. Primero hay que descomponer en factores primos:
40 = 23 · 51
16 = 24
Ahora habrá que tomar los factores comunes elevados al menor exponente. Es decir, 23. Se harán ocho packs, cada uno con cinco bolígrafos y dos pines.
En Nobbot | ¿Recuerdas cómo se hace una ecuación de primer grado?
Imágenes | iStock/delmonte1977, iStock/Maksym Belchenko, iStock/ABBPhoto

