El ser humano teme a lo desconocido, especialmente si se trata de algo que ya lleva la etiqueta de pandemia mundial. La falta de certezas sobre la situación que se está viviendo con la expansión del coronavirus sorprende a jóvenes y mayores, que observan con estupor cómo a diario hay más preguntas que respuestas.
Si hay algo que por su propia naturaleza no falla son las matemáticas. Catalogadas históricamente como ciencia exacta, sus modelos de propagación de epidemias esclarecen un poco esa incertidumbre que ahora oscurece la vida diaria. O, al menos, pueden cuantificarla.
A eso se dedica desde hace una semana el equipo de investigación Munqu del Instituto Universitario de Matemática Multidisciplinar (IMM) de la Universidad Politécnica de Valencia (UPV). Munqu viene de Modelling Uncertainty Quantification; precisamente, cuantificación de la incertidumbre en la modelización. Los resultados que están encontrando pueden servir para concienciar a la población y alertar a tiempo a los médicos.
El engranaje matemático se pone en marcha
A los investigadores del IMM la inspiración les pilló trabajando. “Tenemos experiencia en enfermedades infecciosas, y cuando empezó todo lo del coronavirus se nos ocurrió hacerle un seguimiento con nuestros conocimientos de modelos epidemiológicos”, explica Rafael Villanueva, catedrático de la UPV. Se pusieron manos a la obra e implementaron el modelo computacional.
El matemático cuenta que lo preocupante cuando surge una nueva enfermedad de este tipo “es que el crecimiento no para hasta que se alcanza un ‘pico’, y es importante para el sistema sanitario saber cuándo se va a llegar”. Por eso hacen desde hace ocho días informes diarios donde intentan dilucidar el escenario futuro de la enfermedad, algo muy complicado ya que “todo cambia constantemente”, indica Villanueva.
El Munqu lo forman matemáticos, ingenieros y físicos, que además colaboran con el Área de Vacunas de la fundación de investigación sanitaria y biomédica Fisabio, desde donde han obtenido ayuda de médicos para afinar el modelo. Todos los científicos luchan contra el coronavirus. Porque en ese modelo, aunque sencillo, entran variables de compleja estimación.
Las herramientas que encienden la luz
Y tú, ¿cómo te encuentras ante el coronavirus? ¿Susceptible de contraerlo, infectado, recuperado? Estos son los tres estados que el Munqu analiza para España, la población de estudio que han considerado. Esas tres posibles fases de un individuo que se expone a una epidemia es lo que da nombre al modelo SIR, uno de los más sencillos en epidemiología.
“Los modelos de epidemias suelen ser bastante estándar. A partir ahí, se cambian los parámetros que guían la evolución de la enfermedad. Por ejemplo, las tasas de infección”, indica el doctorando en Matemática Aplicada y miembro del equipo David Martínez.
Se trata de “un modelo de ecuaciones en diferencias, es decir, se estudian en pasos discretos: hoy, mañana, pasado”, indica la investigadora del grupo Clara Burgos. Cada día actualizan el modelo con los datos del Ministerio de Sanidad publicados el día anterior, y cuelgan los informes en su web y en su perfil de Twitter.
El modelo tiene las siguientes ecuaciones:
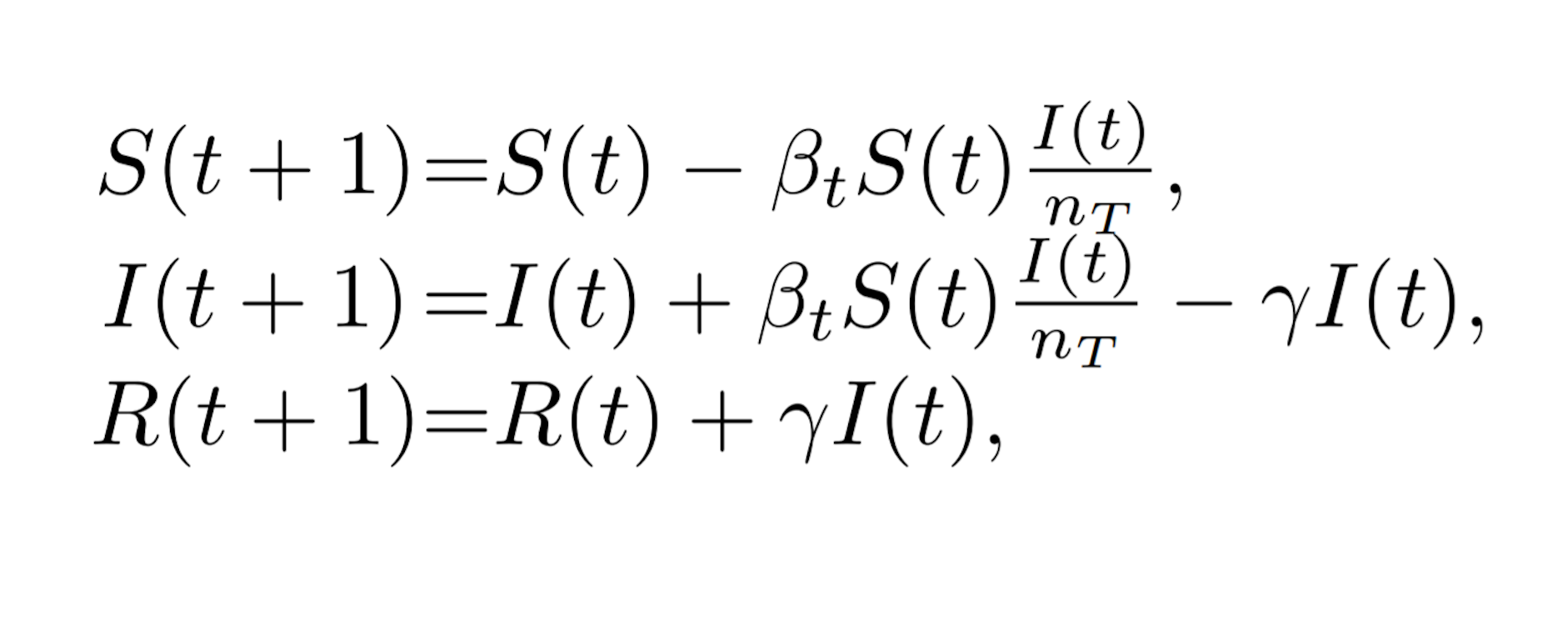
Las expresiones S(t), I(t) y R(t) son funciones matemáticas, relaciones que cambian con el tiempo (representado por t) y que corresponden en este caso a las poblaciones susceptible, infectada y recuperada, respectivamente. Es decir, si tomamos el tiempo t como el día 20 de marzo, S(20 de marzo) será la población susceptible de ser contagiada hoy.
Hay otro factor que depende del tiempo: ?t, la tasa de transmisión del coronavirus. “Este número dice la posibilidad de pasar de un estado susceptible a uno infectado. Viendo cómo se comporta respecto al tiempo podemos predecir qué ocurrirá mañana”, explica Burgos. Por último, el número ? es la tasa de recuperación de la enfermedad (según los médicos que les asesoran, 14 días) y nT corresponde a la población total de España.
Viendo el modelo, si, por ejemplo, queremos estimar qué población estará previsiblemente recuperada el lunes 23 de marzo, la cifra será igual a la población recuperada del día 22 más la población infectada del día 22 multiplicada por la tasa de recuperación.
Con todo esto, se obtiene una estimación de la predicción de la evolución del Covid-19 en España. ¿Y qué dice ahora esa predicción?
Un intervalo para el control del descontrol
Es imposible saber con certidumbre cuántos españoles habrán comunicado que tienen coronavirus el próximo domingo 22 de marzo, pero se puede estimar una cifra que de cierta seguridad. “La cuestión no es acabar con la incertidumbre, la intención es tenerla cuantificada”, señala Villanueva.
En particular, debido a la gran incertidumbre de la situación (depende del comportamiento de la población, de las medidas del gobierno, de la gente infectada que aún no ha manifestado síntomas, etcétera), los investigadores están haciendo estas estimaciones a tres días vista.
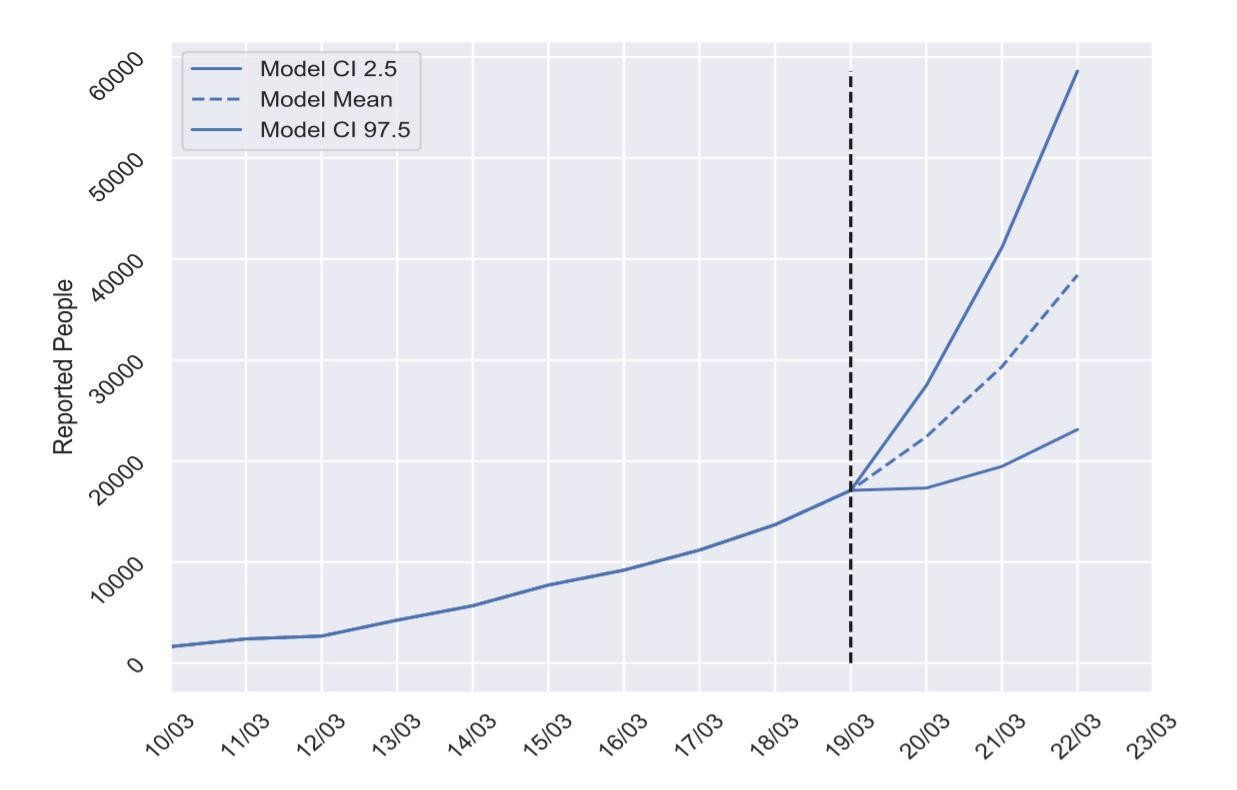
A partir del último día con datos (el eje vertical negro punteado), los investigadores obtienen una gráfica que marca la media de estimación (la línea azul punteada), así como los valores máximo y mínimo (las líneas azules que enmarcan la anterior). El ejemplo superior se basa en los datos publicados hasta el jueves 19, y predice que el domingo una media de 38.417 españoles habrán reportado tener coronavirus. Con bastante seguridad, el escenario se encontrará en el rango dibujado (entre 23.124 y 58.613 reportados).
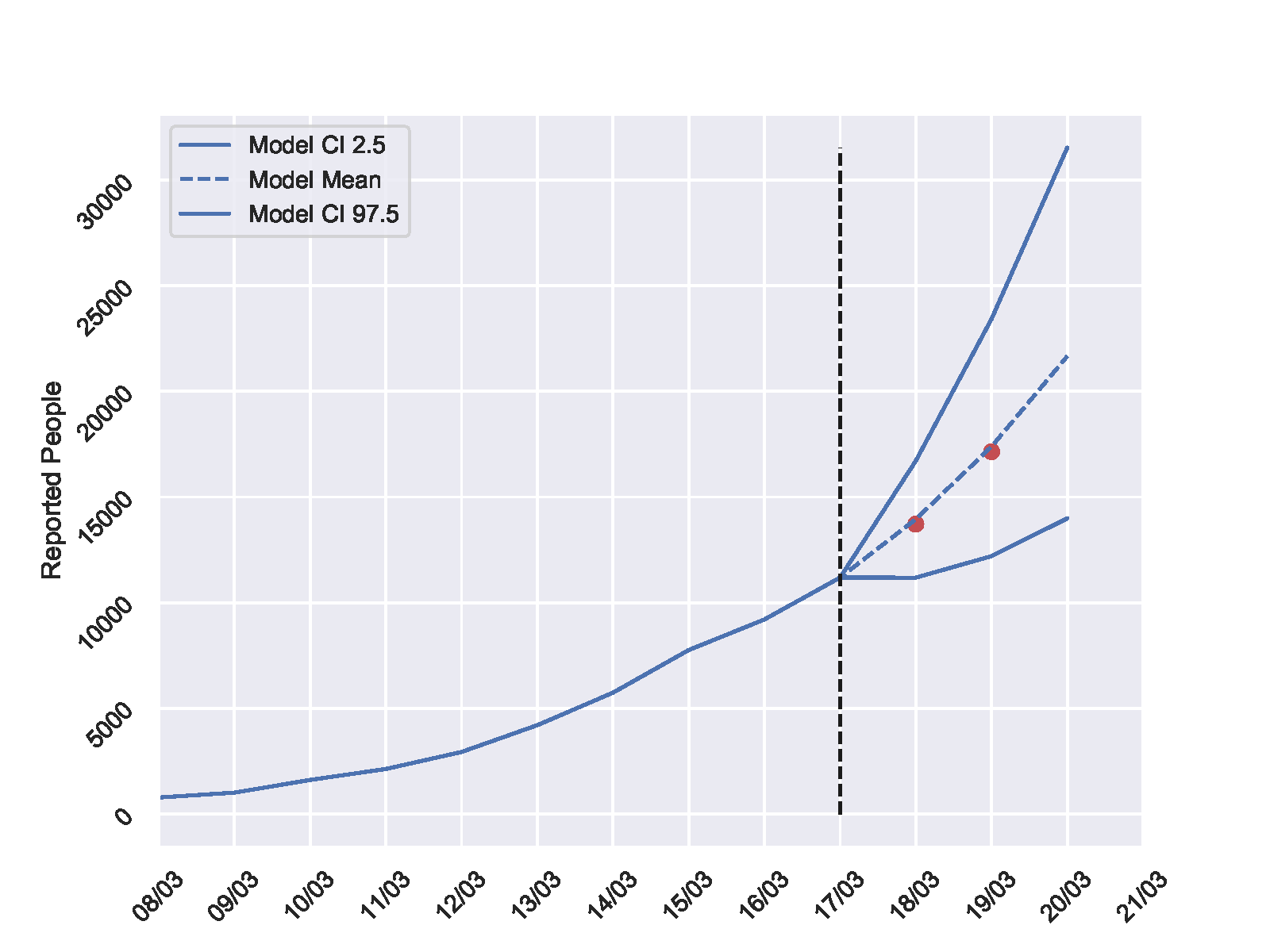
El modelo, cuentan los investigadores orgullosos, de momento se ajusta notablemente bien a la realidad. Para comprobarlo solo hay que echar la vista unos días atrás. Esta gráfica actualizada muestra con puntos rojos el número de casos reportados que se produjeron el 18 y 19 de marzo. Coinciden con la estimación.
Modelo matemático, dime, ¿cuándo se frena esto?
Las predicciones más a largo plazo sobre cuántos españoles pasarán la enfermedad son peliagudas. Las cifras, a priori, parecen alarmantes. El Munqu se atreve a ello con dos objetivos: concienciar a la ciudadanía y afinar el tiro para el sistema sanitario.
“La semana pasada, antes de que se tomaran fuertes medidas, predijimos que se iban a alcanzar casi 4 millones de reportados con coronavirus en las próximas dos semanas. Tenemos que quedarnos en casa”, explica Villanueva. A partir del momento en que se alcanza el pico de infección, la tasa de transmisión bajará y los casos descenderán. En la predicción realizada hace una semana, el 12 de marzo, se observa que ese pico llegaría en torno al 31 de marzo.
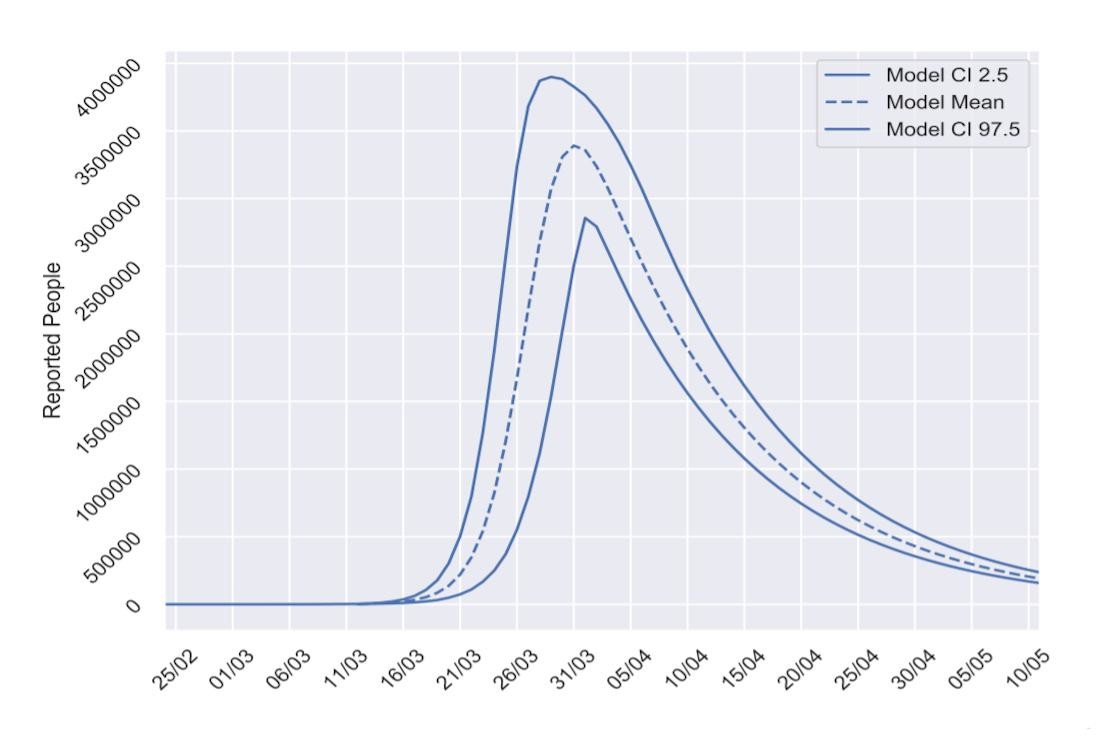
Como la infección tarda de cinco a seis días en hacerse visible en los afectados, los efectos de la cuarentena empezarán a notarse en el modelo con los próximos datos. Sin embargo, según el investigador, sí que se percibe ya que “hace una semana se empezaron a suspender actividades multitudinarias, de ocio y eventos deportivos, y la gente empezó a tomar conciencia y precauciones”.
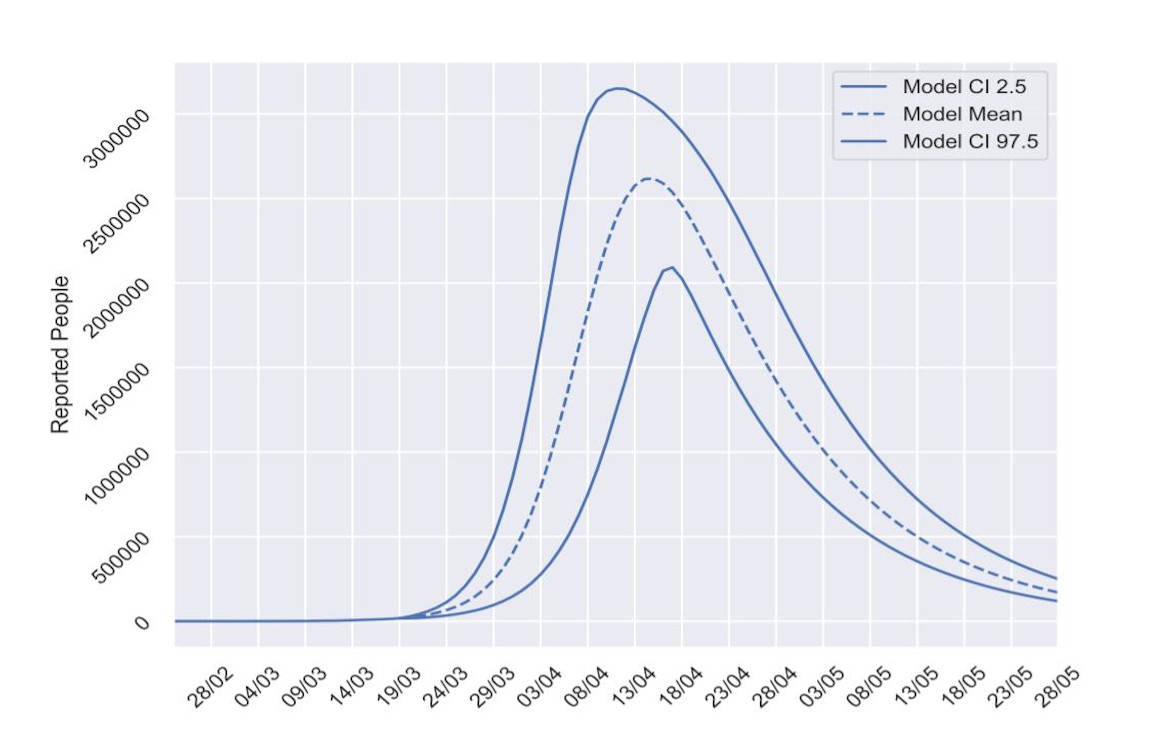
Esto se traduce en que, en la predicción realizada el 19 de marzo, el pico de infectados es más bajo y se ha retrasado en el tiempo. “Que el pico baje y se atrase así implica no saturar tanto el sistema sanitario”, añade Villanueva.
Los datos se modifican cada día y la situación resulta por su propia naturaleza impredecible: depende, en mucha medida, del comportamiento de la gente. Por eso, Martínez resume: “Esa predicción va a cambiar y mejorar si todos somos responsables”. Al menos, eso vaticinan las matemáticas.
En Nobbot | «España lleva unas dos semanas de retraso con respecto a Italia y debe evitar llegar a nuestra situación»

